Now that we have an understanding of Baye’s Rule, let’s try to use it to analyze linear regression models.

Linear regression model is defined as -

Yj = ∑i wj* Xij

Where i is the dimensionality of the data X. j represents the index of input data X. wi are the weights of the linear regression model. Yj is the corresponding output for Xj.
If i = 3,
Yj = w1* x1j + w2* x2j + w3* x3j
Where j is ranging from 1 to N where N is the number of data points we have.

Bayesian Model For Linear Regression

While the process of Bayesian modelling will be taken up in next part, let us consider the below model as true, for now.

P(w,Y,X) = P(Y/X, w) * P(w) * P(X) ….. (4)
Or
P(w ,Y ,X) * P(X) = P(Y/ X ,w) * P(w) ….. (5)
Or
P(w, Y/X) = P(Y/X, w) * P(w) ….. (6)

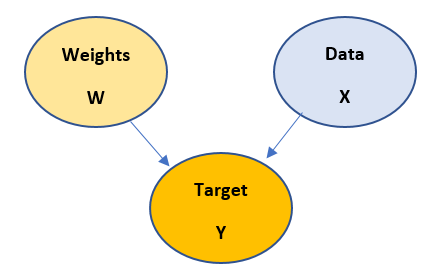
The model shown above is derived from Bayesian model theory and it means that -

Target Y is dependent on Weights W and input data X. And Weights and Data are independent of each other.

Now let us try to build our Baye’s equation for the above model. We aim at determining the parameters of our model i.e. weights w. Thus the posterior distribution with given Xtrain , Ytrain as data looks like:

P(w / Ytrain , Xtrain) = P(Ytrain / w, Xtrain) * P(w) / P(Ytrain / Xtrain) ….. (7)
Here: Likelihood: P(Ytrain / w, Xtrain)
Prior: P(w)
Evidence: P(Ytrain / Xtrain) = constant, as data is fixed
Considering that likelihood is coming from a Normal distribution with mean as wTX and variance as σ2 I the probability density function looks like: P(Ytrain / w, Xtrain) ~ N(Y|wTX, σ2 I)
We have taken σ2 I as identity matrix because of calculation simplicity, but sometimes can take different covariance matrix is considered, which means that different dimensions of the data are intercorrelated.
As a prior distribution on w we take Normal distribution with mean = zero and variance = 1. The probability distribution function can be defined as P(w) ~ N(w|0,1)
Now our Posterior distribution looks like: [ N(Y | wT X ,σ2 I) * N(w | 0,1) / constant ] - we need to maximize this with respect to w. This method is also known as Maximum A Posteriori.

Mathematical Calculation

P(w/Ytrain , Xtrain) = P(Ytrain / w , Xtrain) * P(w) ---- maximizing this term w.r.t w
Taking log both sides-
log(P(w/Ytrain , Xtrain)) = log(P(Ytrain / w , Xtrain)) + log(P(w))
LHS = log(C1 * e( -(y - wTx) ( 2σ2 I)-1 (y - wTx)T )) + log(C2 * e(- (w) ( 2γ2 )-1 (w)T ))
LHS = log(C1) - (2σ2 )-1 * || y - wT X||2 + log(C2) - (γ2 )-1 * ||w||2 -- maximizing w.r.t w
Removing constant terms as they won’t appear in differentiation
Multiplying the expression by -2σ2 and re-writing we get:
= ||y – WTX||2 + λ2 * ||w||2 -- minimizing w.r.t w ---- (8)

The above minimization problem is the exact expression we obtain in L2 Norm regularization. Thus we see that Bayesian method of supervised linear regression takes care of overfitting or underfitting inherently.

Implementation Of Bayesian Regression

Now we know that Bayesian model expresses the parameters of a linear regression equation in form of distribution, which we call as posterior distribution. To compute this distribution we have different methodologies, one of which is Monte-Carlo Markov-Chain (MCMC). MCMC is a sampling technique which samples out the points from parameter-space which are in proportion to the actual distribution of the parameter in its space.

The next post will be around how to build Bayesian models.

This point of view article originally published on datasciencecentral.com. Data Science Central is the industry's online resource for data practitioners. From Statistics to Analytics to Machine Learning to AI, Data Science Central provides a community experience that includes a rich editorial platform, social interaction, forum-based support, plus the latest information on technology, tools, trends, and careers.

Click here for the article